베이즈 정리
개념들
베이즈 정리(Bayes Theorem)
사전확률(Prior Probability)어떤 특정 사건에 관한 선험적 믿음가능도(Likelihood): 주어진 자료를 관측할 확률사후확률(Posterior Probability)자료를 추가하여 사전확률을 업데이트한 확률-
우리는 Pr(A B) = Pr(B A)로 오해하는 경우가 많다 P-value의 경우
귀무가설이 참일때 관측한 검정통계량의 값과 같거나 더 극단적인 값을 가질 확률로 정의하지만,
많은 사람들이 관측된 검정통계량의 값을 기반으로 귀무가설이 참일 확률로 오해한다.
오즈(Odds)
- 어떤 사건이 일어날 확률과 그렇지 않을 확률의 비율
- 사건이 일어날 확률 / (1- 사건이 일어날 확률)
가능도비(Likelihood Ratios)
두 개의 가설 중 어느 가설이 맞는지를 나타내는 비율로, 특정 증거를 수집할 확률의 비율
베이지안 가설검정
기존의 가설검정은 대립가설을 증명하거나 하지 못하는 경우만 결론으로 제시가능
= 귀무가설이 맞는지 여부에 대해서는 이야기를 할 수 없다
- 베이지안 가설검정에서는 귀무가설이 참인지 여부에 대해서 결론을 내릴 수 있다
- 베이지안 가설검정은 전통적인 빈도주의 가설검정과 다르게, 가설에 대한 확률을 직접 계산
- 이 방법은 사전확률(prior probability)을 포함하며, 새로운 데이터를 통해 이 확률을 업데이트
- 가설검정의 결과는 사후확률(posterior probability)로 표현되며, 이는 데이터와 사전 지식을 모두 고려한 확률
베이즈 인자 (Bayes Factor)
BF=P(Data∣H0) / 1)
- 귀무가설(H0)과 대립가설(H1), 사이의 증거 강도를 수치로 나타낸것
- BF>1인 경우, 데이터는 대립가설을 지지하며, <1인 경우 귀무가설을 지지
-
각 가설 하에서 관측된 데이터의 가능도비로 정의
베이즈 인자와 가능도비의 차이점은 가능도에 들어있는 모수에 대해서 이 모수의 사전분포를 이용하여 평균을 계산하는 점
→ 사전분포가 베이즈 인자 계산에 중요한 역할
베타 분포
- 연속 확률 분포의 한 종류로, 두 매개변수 𝛼(알파)와 𝛽 (베타)에 의해 형태가 결정
- 0과 1 사이의 값을 갖는 변수에 대해 사용되며, 특히 비율이나 확률과 관련된 데이터를 모델링할 때 유용
- 유연성: 𝛼, 𝛽 값에 따라 매우 다양한 형태를 가질 수 있습니다. 예를 들어, α=β=1일 때는 균등 분포(Uniform distribution)의 형태를 취하고, α>1 및 β>1일 경우에는 종 모양의 분포
-
매개변수:
𝛼: 성공 또는 긍정적 결과의 “강도” 또는 “수” 𝛽: 실패 또는 부정적 결과의 “강도” 또는 “수”
- 응용: 베타 분포는 베이지안 통계학에서 사전분포(prior distribution)로 자주 사용, 사전분포가 베타분포 일 시에 사후분포 역시 베타분포
예시
도핑 테스트
- 상황 설명: 운동경기에서 도핑 테스트의 정확도는 약 95%로 알려져 있습니다. 이는 테스트의 민감도와 특이도 모두 95%임을 의미
- 문제: 만약 한 선수의 도핑 테스트 결과가 양성이 나왔을 경우, 실제로 그 선수가 약물을 복용하고 있을 확률은 얼마인가요?
- 해결: 1000명의 선수에 대한 기대도수나무를 이용해 계산했을 때, 검사 결과가 양성인 경우는 총 68명이며, 이 중 실제로 약물을 복용한 비율은 19/68 = 약 28%
서울시 관악구 감염성 질환 유병률 조사
서울시 전체 유병률이 10%이고 5%에서 최대 20%까지 분포하고 있을 때,
관악구에서 20명의 표본을 뽑아서 감염 여부를 조사한 결과 아무도 감염이 된 사람이 없었다.
위의 조사 만으로 관악구의 유병률을 0%라고 추정하는 것은 합리적일까?
베이지안 계층모형 사용
-
사전분포: 유병률이 베타분포를 따르며, 평균이 0.10인 것으로 가정
𝛼 = 2 , 𝛽=20
-
가능도: 이항분포를 사용하여 20명 중 감염된 사람의 수를 모델링합니다.
-
사후분포: 베이즈 법칙을 사용하여 계산된 새로운 유병률 추정치입니다.
 HeeYeon Kwon
HeeYeon Kwon 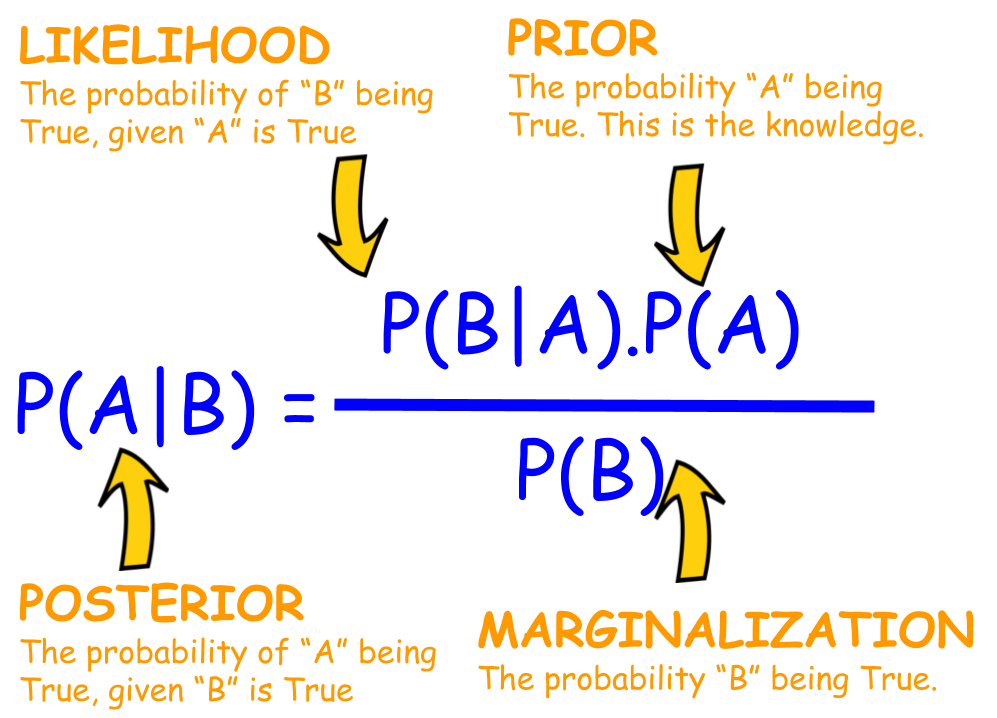
 Hypothesis Testing
Hypothesis Testing