통계학 분야의 3대 진영
- 빈도주의 통계학 (Frequentist Statistics)
- 접근 방식: 장기적인 빈도를 중시, 동일한 실험이 무한히 반복될 경우, 특정 결과가 얼마나 자주 발생할지에 초점
- 확률의 정의 : 사건의 장기적 빈도
- 사전 지식의 배제 : 사전지식이나 믿음을 고려하지 않고 오직 데이터에만 의존
- 가설 검정: 귀무 가설(null hypothesis)을 설정하고, 데이터를 통해 이를 기각할지 여부를 결정
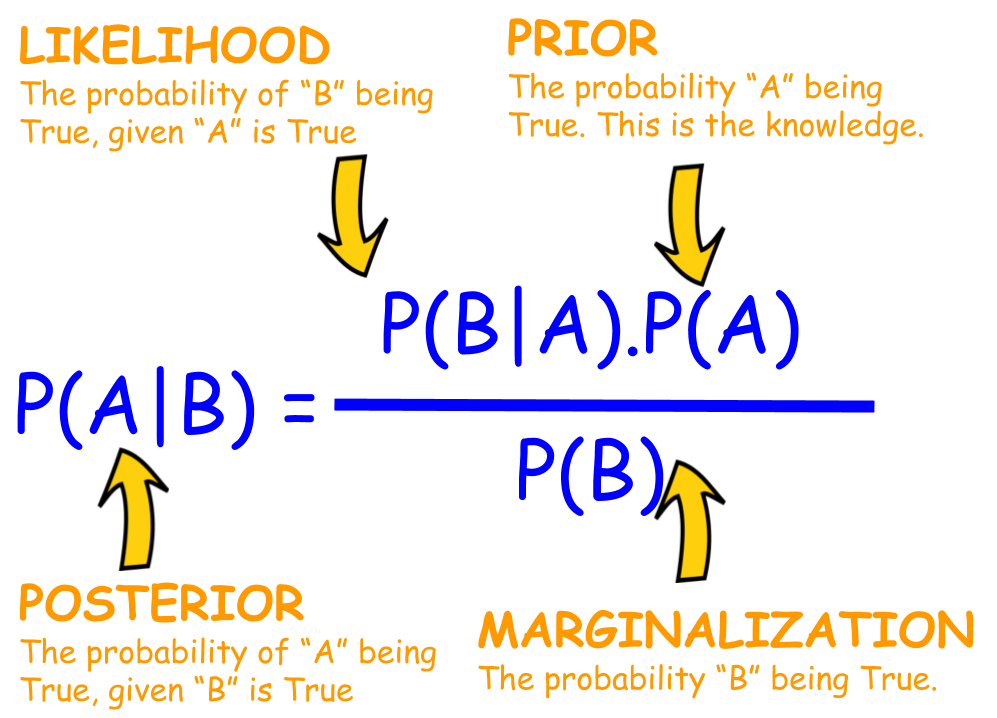
- 베이지안 통계 (Bayesian)
- 접근 방식: 사전 지식과 데이터를 결합하여 추론
- 확률의 정의: 사건의 불확실성 또는 개인의 믿음의 정도로 확률을 정의
- 사전분포의 사용: 사전 지식을 수학적인 형태(사전분포)로 표현하고, 데이터를 통해 이를 업데이트(사후분포).
- 갱신 가능한 추론: 새로운 데이터가 제공될 때마다 추론을 갱신하고 개선
- 피셔리언 통계학 (Fisherian)
- 접근 방식: 론랄드 피셔(Ronald Fisher)에 의해 개발된, 특히 실험 설계와 가설 검정에 중점
- 확률의 정의: 빈도주의적 관점을 따르나, 통계적 유의성에 중점
- 가설 검정의 중요성: 작은 샘플 사이즈에서도 유용하며, 특정 가설에 대한 유의성을 테스트하는 데 초점
- P-값의 사용: P-값을 사용하여 결과의 유의성을 평가합니다.
가설검정의 절차
1st 가설설정
-
귀무가설기본적인 가정으로, 일반적으로 검증하고자 하는 효과가 없다는 가설 -
대립가설우리가 증명하고자 하는 가설을 의미
2nd 검정통계량의 표본분포
검정통계량
샘플 데이터를 요약하여, 귀무 가설이 참인지를 판단하는 데 사용되는 단일 수치, 검정통계량의 분포로 귀무가설이 참이라는 가정하에 검정통계량의 값이 극단인지 여부를 판별 가능
검정통계량의 분포는 아래 3가지를 따른다.
1 카이제곱분포
sum (관측치 - 귀무가설하에서 기댓값)^2 / 관측값)
- 정의 : 표준정규분포를 따르는 확률변수의 제곱이 자유도가 1인 카이제곱분포를 따른다
- 자유도 : (행의 갯수 -1) * ( 열의 갯수 -1)
- 서로 독립인 카이제곱분포의 합은 역시 카이제곱분포를 따르며 이 경우 자유도는 합치기 전 각각 확률변수의 자유도의 합과 같다
2 t-분포
(관측치 - 귀무가설하에서 기댓값) / 표준오차
- 정의 : 모집단이 정규 분포를 따르지만 분산이 알려져 있지 않고 표본 크기가 작은 경우에 적용되는 분포
- 특징 : 정규분포와 비슷한 모양으로 0을 중심으로 대칭이며 꼬리 부분이 두터운 모양
3 표준정규분포
카이제곱분포, t- 분포의 경우 자유도를 모수로 가진다 → 자유도가 커지면 두 분포는 정규분포의 모습과 비슷
3rd p-value와 유의수준 계산
1)p -value
귀무가설이 참이라는 전제하에 우리가 관측한 검정통계량의 값이나 혹은 그보다 더 극단적인 값을 얻을 확률
양측검정인지 단측검정인지 여부에 따라 검정통계량의 분포를 이용하여 p-value 계산
가설검정에서 과학적인 근거가 있지 않은 한 **양측 검정**을 하는 것이 원칙!
ex ) 신약 개발시 제약회사는 항상 신약이 병을 낫게 할 것이라고 하지만
반대로 신약이 병을 악화시킬 가능성도 있기 때문에 FDA에서는 항상 양측검정 시행
2)유의수준
귀무 가설을 기각하는 기준이 되는 확률값
❗ 가설 검정의 전략은
제 1종 오류를 범할 확률을 알파이하로 하고 검정력(1-b)을 최대로 하는 결정 찾기
-
흔히 사용하는 유의수준 a=0.05이며 검정력은 0.80이다.
즉 새로운 신약이 치료효과가 있는지 검정하기 위해서는 치료효과가 없을 때 귀무가서을 기각할 확률은 0.05 이하이어야 하고 치료가 효과적일 때 치료효과가 있다라고 결론 내릴 확률이 80% 이어야 한다.
-
검정력은 표본의 개수가 커질수록 증가하기 때문에 원하는 검정력을 얻기 위해서 어느 정도의 표본이 필요한지 미리 계산 가능
다중검정
- 만약 귀무가설이 참인 두 번의 가설검정에서 적어도 한 번은 p-value가 0.05보다 작을 확률은 1-0.95^2 -0.0975로 거의 10%에 육박
- 이런 다중검정 문제는 연구자들이 데이터를 여러 개로 쪼개서 각각에 대해 가설 검정을 한 후 유의미한 결과를 발표할 때 생기는 문제
-
교정 방법 : 100개를 기각했을 때 10개를 잘못 기각한 경우 vs 50개를 기각했을 때 6개를 잘못 기각한 것 중 어느 것이 더 심각한 실수인지에 따라 선택
-
가장 보편적인 p-value 교정 방법은
Bonferroni 교정기준이 되는 유의수준 / 전체 가설검정의 횟수
-
Bonferroni 교정은 너무 엄격한 기준잣대를 사용하고 있어 다른 교정방법으로 오발견율(False Discovery Rate)를 통제
오발견율(False Discovery Rate)전체기각된 가설검정의 개수 중 잘못 기각한 경우의 비율 (False positive 비율)
-
4th 귀무가설 기각 여부
p-value가 주어진 유의수준보다 작은 경우 귀무가설하에서 이러한 결과를 얻을 가능성이 극단적이라고 생각하고 귀무가설을 기각
예시
❓ 팔짱을 낄 때 어느 팔이 위로 올라가는가 ?
남녀 별로 팔짱 끼기 차이가 없다는 가정하에 54명에게 조사를 했을 때
남녀 간 7%의 차이가 났을 때 이 차이가 관측하기 힘든지 여부를 어떻게 판단할까.
1 순열검정으로 가설검정
순열 검정
-
두 개 이상의 집단 간의 차이가 우연에 의한 것인지를 판단하기 위해 사용되는 비모수적 통계 검정 방법
-
이 방법은 원래 데이터의 순서를 무작위로 바꾸어(순열) 여러 번 재배열하여, 관찰된 데이터가 무작위로 발생한 것인지 아니면 통계적으로 유의미한 패턴을 보이는지를 평가
1st 가설설정
2nd 순열검정(Permutation Test)
위의 실험을 1000번 반복한 후 비율의 차이를 히스토그램으로 그렸을 때(비율의 차이에 관한 표본분포) 히스토그램 중앙의 점선이 실제 설문 결과였던 7%를 나타낸다.
3rd 남녀간 오른팔이 위에 있는 비율의 차이가 0.07 이상인 경우에 해당하는 비율이 p-value에 해당
그림에서 점선 오른쪽 꼬리 부분의 넓이를 계산하면 p-value가 0.45
대립 가설 “ 성별로 팔짱 끼는 방식이 다르다 “
검정통계량의 값은 음수로 나올 수 있기 때문에 양측검증을 하여서 p-value가 0.90이 된다
대립 가설이 “ 여성이 남성보다 팔짱을 낄 때 오른팔을 올려놓는 것을 선호한다 “ 라면
단측검정을 하며 p-value가 0.45가 된다
2 카이제곱검정을 이용한 독립성 검정
순열검정 방식보다 일반적인 방식
1st 가설설정
2nd 검정통계량의 값은 0.2, 자유도가 1인 카이제곱 분포를 따르고
3rd p-value가 0.90 이므로
conclusion 귀무가설을 기각할 수없다
서로 독립인 두 집단 비교하기 2-표본 t- 검정
1st boxplot으로 두 그룹 비교
2nd 가설설정
귀무가설은 두 집단의 평균은 차이가 없다
3rd 검정통계량 설정
( 추정치 - 귀무가설하에서 추정하고자 하는 모수의 값 ) / 표준오차
표준오차의 경우 두 집단의 분산이 같은 경우와 다른 경우 2가지를 고려
-
일반적으로 두 집단의 분산이 다르다고 보는 것이 타당하고, 선행연구나 분산이 같다는 가정이 합리화 될 수 있는 경우에 사용하는 것이 타당
→ 데이터를 관측한 후에 어떤 방법을 사용할지 정하는 것이 아니라 미리 분석방법을 결정!
- 표준오차의 자유도
- 두 그룹의 분산이 같은 경우 : na + nb -2
- 두 그룹의 분산이 다른 경우 : 프로그램을 사용하여 구하기, 일반적으로 두 그룹의 표본크기 중 최솟값보다 크다
- 추정하고자 하는 모수는 두 집단 평균의 차이 → 추정치는 표본 평균의 차이
4th p-value 계산
검정통계량이 정규분포 따르는지에 따라 2가지를 고려
- 정규분포 X → 순열검정 이용
- 정규분포 O → t- 분포 이용
- 먼저, 히스토그램으로 정규분포 따르는지 확인
- 모집단이 정규분포를 따른다면 검정통계량은 t-분포
쌍으로 주어진 2개의 집단 비교하기 Paired t- test
2 표본 검정에서는 2개의 표본이 서로 독립이라는 가정이 있는데, 쌍으로 주어진 데이터는 서로 독립이 아니다.
1st 가설설정
쌍으로 주어진 데이터 차이들의 평균이 아주 극단적인 값을 가지는 경우 귀무가설을 기각
2nd 검정통계량 설정
( 추정치 - 귀무가설하에서 추정하고자 하는 모수의 값 ) / 표준오차
= (차이의 평균 - 0) / (표준편차/루트 (표본 수 *2 -2))
2개 이상의 집단 비교하기 분산분석(ANalysis Of VAriance)
1st 가설설정
귀무가설 : 각 그룹의 평균은 동일하다
대립 가설 : 각 그룹별 간 평균은 같지 않다
2nd 검정통계량 설정
귀무가설하에서 검정통계량은 F분포를 따른다
F 분포
- F = 그룹 간의 평균의 변동 / 그룹 내의 평균의 변동
- 정규분포를 이루는 모집단에서 독립적으로 추출한 표본들의 분산비율이 나타내는 연속 확률 분포
- F ( 분자의 자유도(K-1) , 분모의 자유도(n-K) ) → 2개의 모수 존재
 HeeYeon Kwon
HeeYeon Kwon 
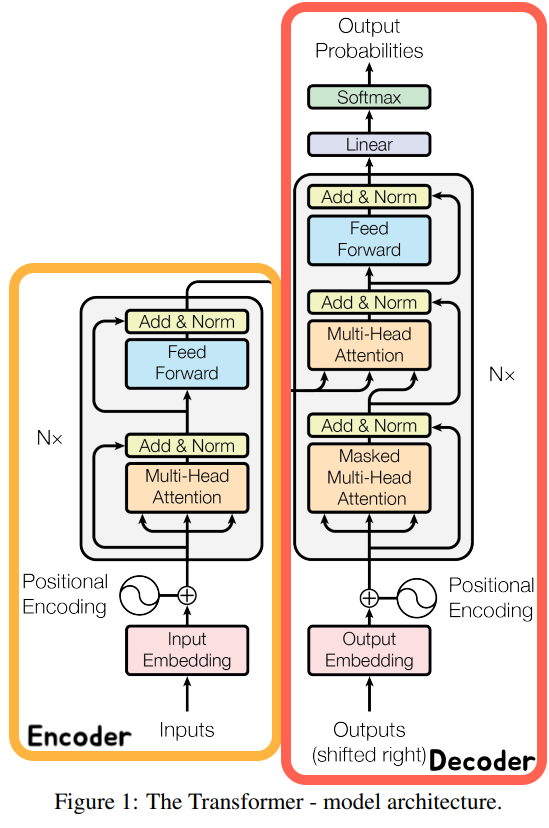 Paper Review : Attention is all you need
Paper Review : Attention is all you need